1
投資
隨著金融危機的發生，金融業界越來越重視金融風險的控制，現在金融風險管理已經成為金融數學研究中的一個重要分支。本文討論的布萊克-斯科爾斯方程給了還沒完成的金融合約低價的理性依據，開創了複雜的投資新時代，催生出了巨大的全球金融產業。
在 Black-Scholes 公式中，符號表示這些變量：
- σ=標的資產的回報波動/期貨，S =其現貨價格 (當前) ;
- δ=變動率，V =金融衍生品的價格;
- r =無風險利率;
- t =時間。
這是投資者的必殺技 (holy grail) 。Black-Scholes 方程式，這是經濟學家 Fischer Black 和 Myron Scholes 的心血結晶，提供一個合理給未履行完的財務契約定價的方式。就像在比賽中途買進或賣出一匹馬的賭注。它開闢了一個新的，且越來越複雜的投資環境，綻放成一個巨大的全球性行業。但是當次級抵押貸款(sub-prime mortgage)市場變壞，金融市場的寵兒變成永無止境地吸吮金錢的’黑洞’。
任何關注危機的人就會明白企業和商品實體經濟，被稱為衍生產品的複雜金融工具搶占風頭。這些不是金錢或貨物。而是投資中的投資，投注中的投注。衍生工具創建了一個繁榮的全球經濟，但同時也導致市場動盪，信貸緊縮，銀行體系瀕臨崩潰和經濟衰退。正是 Black-Scholes 方程式開闢了衍生工具的市場。
方程式本身不是真正的問題。它是實用的，精確的，其局限性也明確指出。它提供了一個行業標準的方法來評估金融衍生品的可能價值。因而衍生品可以在它們成熟之前買賣。如果明智地使用它，並在市場條件不適用時放棄它，該公式是好的。麻煩的是其潛在的濫用。它允許衍生工具成為以它們自己的方式交易商品。金融部門把它叫做Midas 公式，視它為可使一切都變為黃金的配方。但市場忘了 Midas 國王的故事是如何結束。
Black-Scholes 支撐大規模的經濟增長。到 2007 年，國際金融體系中的交易衍生品價值為每年一兆美元。這是世界製造業在過去一個世紀所有產品創造價值總值的 10 倍 (調整通貨膨脹後) 。更加複雜的金融工具其發明的缺點是，其價值和風險越來越不透明。因此，公司聘請了有數學才能的分析師，制定類似的公式，來告訴他們這些新工具的價值和它們的風險。不好的是，他們忘了問當市場條件改變時結果的可信度。
Black 和 Scholes 在 1973 年發明的方程，Robert Merton 不久後提供了額外的評論。它適用於簡單，古老的衍生工具：期權。主要有兩種：認沽期權賦予買方有權在指定的時間以商定的價格出售商品。看漲期權是相似的，但它賦予的權利，是買，而非賣。方程提供了一個系統化的方法來計算到期前期權的價值。期權可以在任何時間出售。因方程式的高效，Merton 和 Scholes 贏得了 1997 年的諾貝爾經濟學獎。 (當時Black已去世，他無資格參選。)
(1997 年諾貝爾經濟獎得主 Merton 與 Scholes)
任何人都會同意，如果每個人都知道衍生工具的精確價值，人們怎麼賺錢？該公式需要用戶估計數值的數量。但用衍生產品賺錢的主要方式，就是買後以更高的價格賣出。贏家從失敗者中奪取利益。在過去的任何時期，有 75％ 和 90％ 之間的期貨貿易商都賠了錢。當次貸泡沫破滅時，全球的銀行失去了數百、數十億美元。在隨後的恐慌中，納稅人被迫依據法案，但法案是政治，而不是數理經濟學。
Black-Scholes 公式涉及四個量化指標。三個可以直接測量：時間，安全期貨資產的價格，無風險利率。這是理論的利率，指投資人可以零風險賺取利潤，如政府債券。第四個量是該資產的波動性。這是描述市場價值變化的不穩定。該公式假定資產的波動性保持不變，這是需要修正的。波動可以通過價格變動的統計分析來測定，但它不能精確測量，不能保證萬無一失，測量與現實不相符合。
許多金融模型背後的想法，可以追溯到 1900 年的 Louis Bachelier，他認為股市波動可以用被稱為布朗運動的隨機過程來建模。在每一個瞬間，股票價格或者增加或減少，該模型假定這些事件有固定的機率。它們可能是相等的，或某一個會比其它的可能性大。這就像人站在街道上，反覆擲硬幣來決定是否向前移動一小步或向後，他向前向後反覆無常。他的位置對應股票價格，隨機上漲或下跌。布朗運動的最重要統計特徵，是它的均值和標準差。均值是短期的平均價格，通常在一個特定的方向漂移，上升或下降取決於股市。標準差可以認為是價格偏離均值的平均量，它有標準的統計公式來計算。對於股票價格，這被稱為波動，它衡量價格波動的穩定性。在時間價格圖上，波動對應鋸齒狀的曲折走勢。
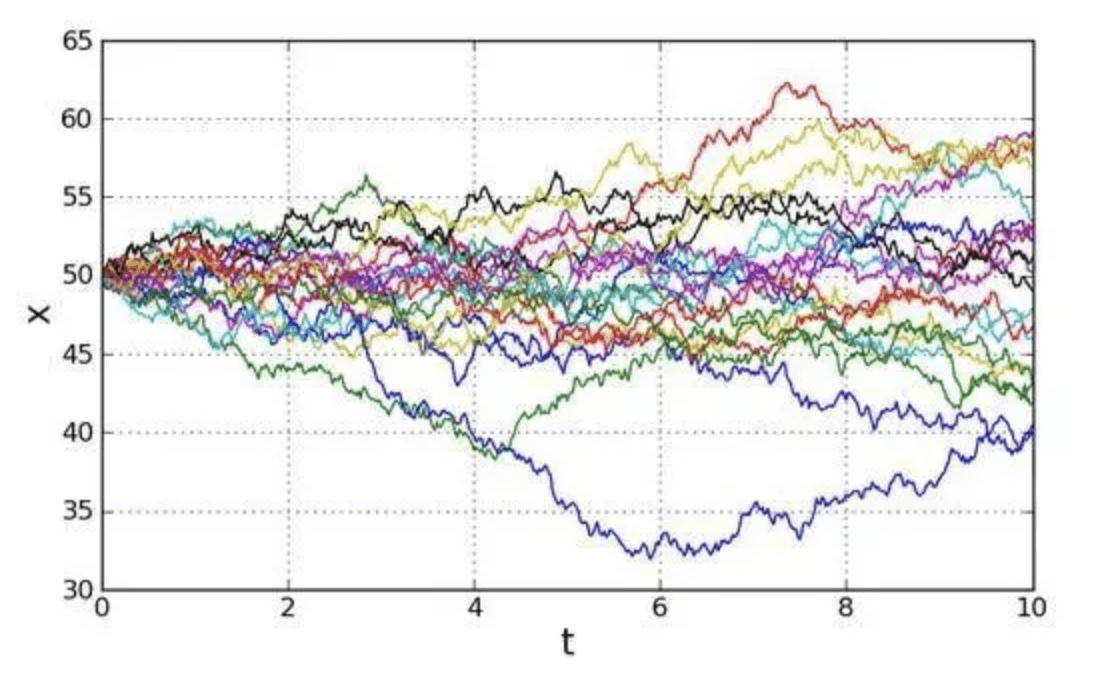(布朗運動)
Black-Scholes 實現巴舍利耶的想法。它不直接給出期貨的 (它應該被出售或購買的) 價格。這是數學家稱為的偏微分方程式，表現了其它變量變化時價格的變化率。方程式提供了具體的認沽期權的價值公式，看漲期權公式。
Black-Scholes 的早期成功，鼓勵金融部門發展一系列針對不同金融工具的相關方程式。傳統銀行可以利用這些方程式，評估貸款和交易，預測潛在的麻煩。但是，很多傳統銀行沒那麼謹慎。很快，銀行也隨之放行越來越多的投機企業。
任何現實的數學模型都依賴於簡化和假設。建立在套利定價理論基礎上的 Black-Scholes 方程式，其中浮動和波動是不變的常數。這個假設在金融理論中很普遍，但對真正的市場往往是不正確的。方程式還假定沒有交易成本，賣空沒有任何限制，錢總是可以以一個已知的、固定的、無風險利率借出和借入。但現實往往是非常不同的。
因為股市大波動應該是極為罕見的，這些假設是有效的，風險通常也很低。但 1987 年 10 月 19 日，黑色星期一，全球股市在幾個小時內失去超過 20％ 價值。根據模型的假設，這種極端事件幾乎是不可能的。金融數學方面的專家，塔雷伯(Nassim Nicholas Taleb)，在他的暢銷書《黑天鵝》中，稱之為黑天鵝般的極端事件。
股市的大幅波動是比布朗運動的預測更為常見。原因是不切實際的假設，並忽視潛在的黑天鵝。但通常模型非常適用，隨時間的推移信心也增強了，許多銀行家和交易員忘了該模型有其侷限性。他們把使用的公式作為一種護身符，如果出了差錯，數學魔術可以保護他們免受批評。
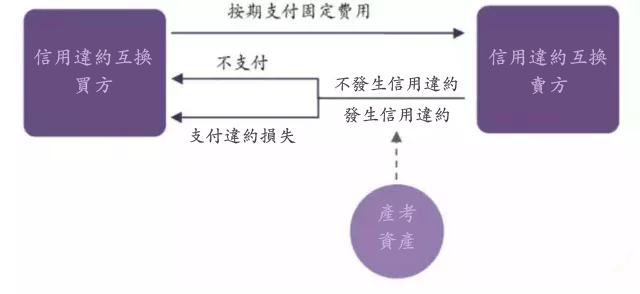
銀行，對沖基金和其他投機者很快就在以大數量交易複雜的衍生工具，如信貸違約掉期 (credit default swaps) 。它們定價後也視為資產。這意味著它們可以作為其他採購的安全支付工具。當一切都變得更複雜，模型用來評估價值和風險，已經與現實偏離越來越遠。某處下面是房地產，市場假定屬性將保持永遠上升，故這些投資無風險。
Black-Scholes 方程式在數學物理中是有解的。這種模型在金融世界中可能是不恰當的。傳統的數理經濟學並不總是符合現實，它失效時會嚴重失效。因此，物理學家、數學家和經濟學家都在尋找更好的模型。
在這些努力的最前沿，是複雜性科學 (complexity science) ，一個新的數學分支，把市場建模為一個按照指定規則的個人相互作用的集合。這些模型顯示一哄而起的群體心理 (市場交易商複製其他市場交易者行為) 的破壞性影響。幾乎每個在上個世紀的金融危機，都是被一哄而起的群眾推到邊緣的。它使一切在同一時間破產。如果用工程師們的看法，一架橋樑倒下，其它所有的也會倒下。
通過學習生態系統，知道經濟模式的不穩定是常見的，主要是因為金融體系的設計不良。用點擊鼠標來轉移數十億美元的設施，可能會帶來越來越快的利潤，但它也使股市衝擊的傳播更快。
金融崩潰應歸咎於方程式？該還是不該。Black-Scholes 可能導致崩潰，但僅有當它被濫用時。在任何情況下，方程式僅是一個存在於不負責任的金融、政治無能、激勵倒錯和監管不嚴的豐富燉湯中配料的一種成分。
儘管其所謂的專業知識，金融部門沒有比隨機猜測所執行得更好。股市已經度過了 20 年，不知路向何方。該系統太複雜，以致不能依據錯誤預感和直覺運行，但目前的數學模型不能充分代表現實。整個系統是知之甚少，岌岌可危。世界經濟迫切需要進行大刀闊斧的改革，那需要更多的數學，而不是更少。這可能是火箭科學 (rocket science) ，但它不是魔術。
《雪球》授權轉載
【延伸閱讀】
57959
