一項新技術,比如電動汽車,進入市場時,消費者會決定他們是否要使用這個新產品。根據接受創新的傾向,可以將消費者分為 “ 早期採用者 ” (adopter)和 “ 落後者 ” (laggard)兩類。美國佛羅里達州立大學的Bhargav Karamched在Physical Review Letters上的最新論文,針對該現象提出了一個網路模型。該模型發現,落後者可以幫助整個群體做出更有益的決定,而不會延緩決策過程。該研究為影響群體智慧的因素,給出了新的洞見。

一、基於隨機遊走的群體決策的缺陷
在過去的幾年裡,統計物理學已經幫助研究人員開發了社會物理學模型,來描述由相互作用因子構成的複雜系統。例如,有些模型揭示了人類社會觀點的動力學 ,以及語言和方言的演變 。
所有這些模型的一個核心組成部分是隨機遊走——一系列隨機步驟產生的路徑。例如當探員蒐集資訊時,可以上下行動。這意味著以前的模型儘管已經研究了決策的不同影響,但是通常忽略了個人在決定自己的想法時是如何考慮他人的決定的。
在一個富裕且環保意識強的社會裡,對新產品的接受會隨著時間的推移而增加,促使大多數人支持一個能夠最大化社會效益的決定,例如採用電動汽車。然而,個人的決定是不可預測的:它們可能取決於特定的這一天的心情。
因此,是否使用新產品,遵循一種 “ 有偏見的 ” 隨機遊走:當朝著承擔社會責任的結果演變時,並不會朝著結果直線前進,而是沿著它的方向波動。決定這個隨機過程是否及何時達到某個臨界點——即觸發購買電動汽車的決定——就是所謂隨機過程中的首次到達問題(first-passage problem) 。
傳統的社會物理學處理決策過程,是通過描述信念的演變規則來實現的。其來源於擬合經驗數據或訴諸來自經驗的原則 。這些方法成功地再現了集體決策的一些特徵,但不能解釋與這些進程相關的許多心理機制。
二、基於貝氏的決策模型
Karamched和他的同事建立了一個以貝氏統計為基礎的模型,來描述一小群人的決策如何能夠向其他尚未決定的人提供資訊。貝氏統計是一個數學框架,通常應用於事件發生的機率取決於先前的信念或與事件相關知識的過程。有證據表明,人類的推理和決策過程可以被模擬為貝氏推斷,這反過來又促進了模擬人類大腦認知功能的人工智慧算法發展 。
Karamched 的這項研究證明,私人資訊的累積相當於一種隨機遊走,由一種持續的力量驅動著每個人的偏好朝著大多數人喜歡的結果方向行動。
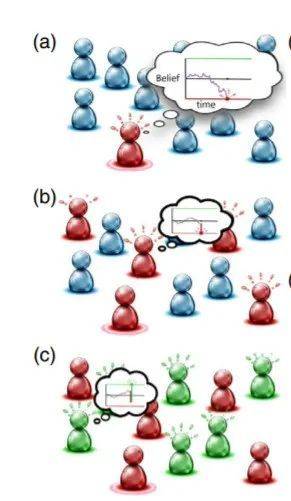
▲群體決策模型,紅色為早期採用者,逐漸說服藍色的未決定者,而綠色為落後者
在其模型中,一個主體(agent)在信念足夠強的情況下做出決定:如果偏好達到一個閾值+θ,主體會做出有利的選擇;如果達到-θ,主體會選擇不那麼有利的結果。θ的值取決於不同的個性:對於早期採用者來說,θ的值很小,對於落後者來說,θ的值很大。
最初,所有的主體都還沒有決定,偏好服從隨機分佈。由於一些主體的個別研究,偏好的分佈將慢慢向有利的決定傾斜。而只要有一個人做出決定,其他人就會看到這個決定,並且受到影響。
在研究者的模型中,觀察者通過調整決策者的閾值(+θ或-θ)來做出反應。接下來會發生什麼取決於人口是同質的(所有人都有相同的閾值)還是異質的(有早期採用者和有不同閾值的落後者的混合)。
三、同質和異質,如何影響群體決策
對於一個同質化的社會,如果第一個決策者選擇了有利的選擇,那麼他將說服任何一個滿足決策閾值的人做出同樣的決定。由於傾向於有利的決定,稍微過半的人屬於這一類,這將說服其餘的人 “ 第一個決定是一個好的決定 ” 。
另一方面,如果第一個決策是不利的,那麼具有對社會不利偏好的人會跟隨領導者,但這些人不會達到總人口的一半。在此基礎上,尚未決定的人可以推斷出第一個決策是不利的,並選擇相反(有利)的那一個。儘管最初的決定很糟糕,但是最終多數人仍會做出最有利的選擇。
如果社會被分成早期採用者和落後者,決策動力學將是不同的,如下圖所示。在這個模型中,當早期使用者做出決定時,落後者會根據早期使用者的閾值,大幅縮小自己的決策閾值。
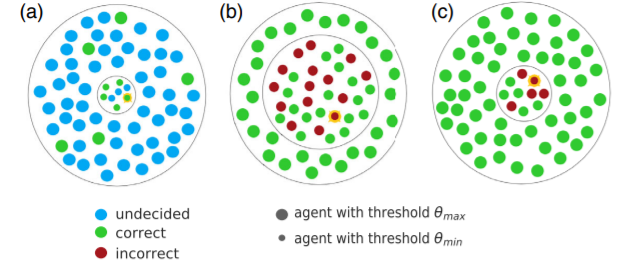
▲決策閾值更低的人,在最初的浪潮後,就會效仿早期採用者
假設在一群尚未決定的人(藍色)中,早期採用者(紅色)做出了一個糟糕的決定。看到這個決定,一組早期採用者也跟著做,但是決策閾值稍大一些的早期採用者(綠色)選擇了最有益的解決方案。在觀察了早期採用者的決策之後,落後者做出了決定,導致很大一部分人糾正了最初那個糟糕的決定。

▲早期採用者(紅色)和落後者(藍色)組成的社會如何做出集體決策
換句話說,落後者認識到一個早期採用者的決定是草率和不可靠的,並給予較小的權重。因此只有早期採用者會受到第一個決定的強烈影響。而落後者只在有足夠數量的早期採用者跟隨第一個決定者時,才會做出反應。然後更小的探索團體將形成,嘗試更多可能的決定,並提供回饋,落後者可以據此決定是否跟隨。
四、總結
該模型表明了落後者的懷疑態度,是如何通過基於更可靠的數據做出集體決策,從而促進更大的利益。即使最初的決策很糟糕,佔更大比例的落後者最終會做出有利的選擇。
儘管如此,早期採用者仍然是必不可少的:如果沒有他們草率的決定,就沒有資訊可供落後者利用。此外,早期採用者決策的速度加快了集體決策的速度,這遠比讓落後者單獨通過緩慢的個人研究過程累積資訊快得多。研究人員發現,對於不同的人口情況,各自存在最佳的採用者-落後者比例,使決策結果最大化。
設計實驗或觀察來測試異質群體是否在現實世界中做出群體利益的決定是很有趣的,正如新模型所預測的那樣。懸而未決的問題是一個關鍵的模型假設是否合理:人們是否真的能夠將較低的權重分配給早期採用者的第一個有風險決定?
公共衛生運動的經驗表明,情況可能是這樣的:與早期採用者相比,鎖定落後者通常被證明更為有效。然而由於前者其創新性,往往被社會投入了過多關注,而忽視了鎖定落後者的影響。目前,廣泛採用健康措施和行為改變(例如戴口罩)是至關重要的,來自Karamched的模型,或許可以幫助公共衛生活動人士確定應該以誰為目標、最有效地傳播他們的資訊。
參考資料:
- C. Castellano, “ Statistical physics of social dynamics, ” Rev. Mod. Phys. 81, 591 (2009).
- RA Blythe, “ Colloquium: Hierarchy of scales in language dynamics, ” Eur. Phys. J. B 88, 295 (2015).
- S. Redner, A guide to first passage processes (Cambridge University Press, Cambridge, 2001)
- EM Rogers, Diffusion of innovations (Free Press, New York, 2003)
- SJ Gershman et al., “ Computational rationality: A converging paradigm for intelligence in brains, minds, and machines, ” Science 349, 273 (2015).
《虎嗅網》授權轉載
【延伸閱讀】





