1
財管
最近在網路上看到一個很有趣的問題：房間裡有 100 個人，每人都有 100 元，他們在玩一個遊戲。每輪遊戲中，每個人都要拿出一元錢隨機給另一個人，最後這 100 個人的財富分佈是怎樣的？
以下是三個不同的答案，請投票：
我們不妨把這場遊戲視作社會財富分配的簡化模型，從而模擬這個世界的運行規律。我們假設：每個人在 18 歲帶著 100 元的初始資金開始玩遊戲，每天玩一次，一直玩到 65 歲退休。“每天拿出一元錢” 可理解為基本的日常消費，“獲得財富的機率隨機” 是為了簡化模型。以此計算，人一生要玩 17,000 次遊戲，即獲得 17,000 次財富分配的機會。
下面我們來回答一下，在上述規則下，遊戲運行 17,000 次的結果如下圖所示：
開始時（第 0 次）：
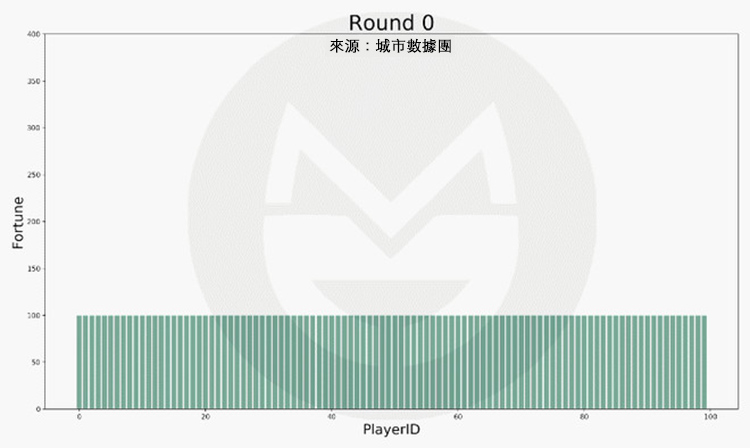
過程中（第 1,200 次）：
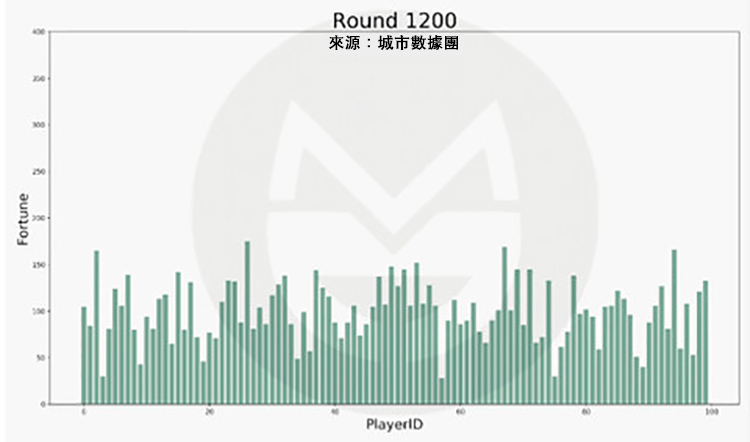
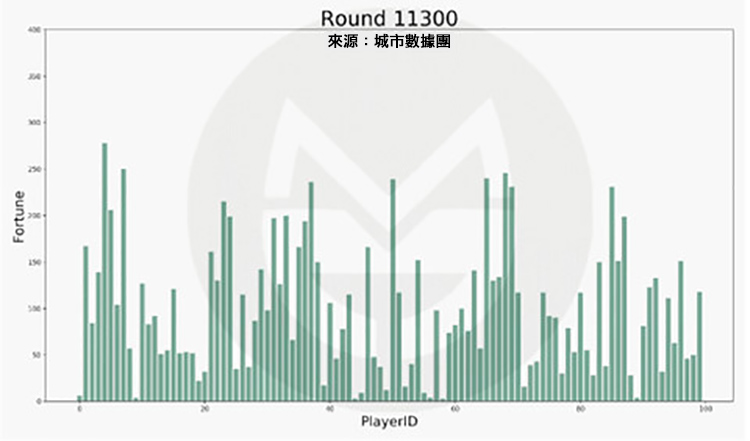
過程中（第 11,300 次）：
結束時（第 17,000 次）：
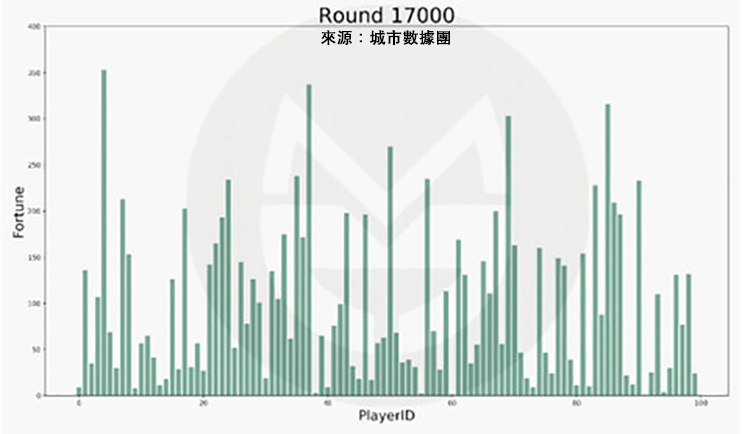
（說明：1、上圖中橫軸標籤代表一個玩家的編號，柱子的高低變動反映該玩家財富值的變化。2、當某人的財富值降到 0 元時，他在該輪無需拿出 1 元錢給別人，但仍然有機會得到別人給出的錢。）
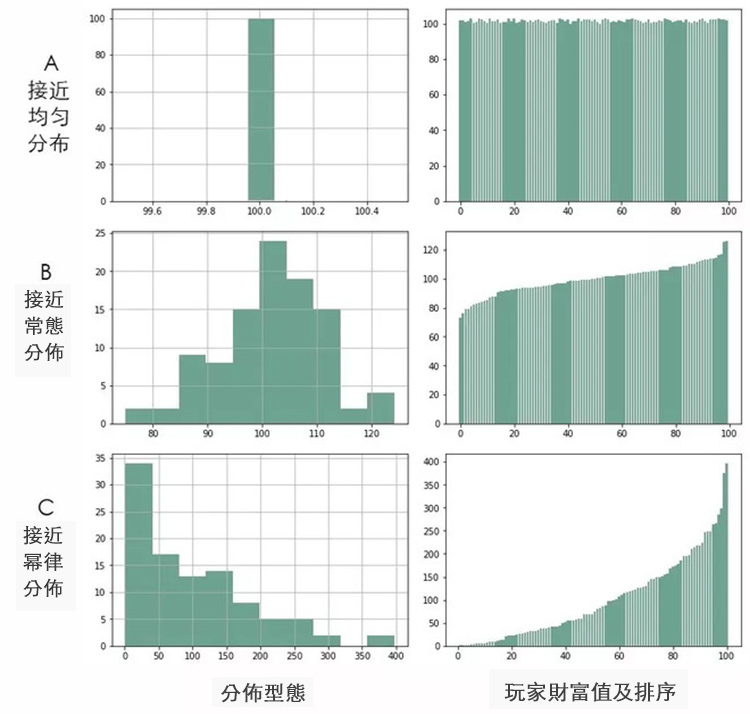
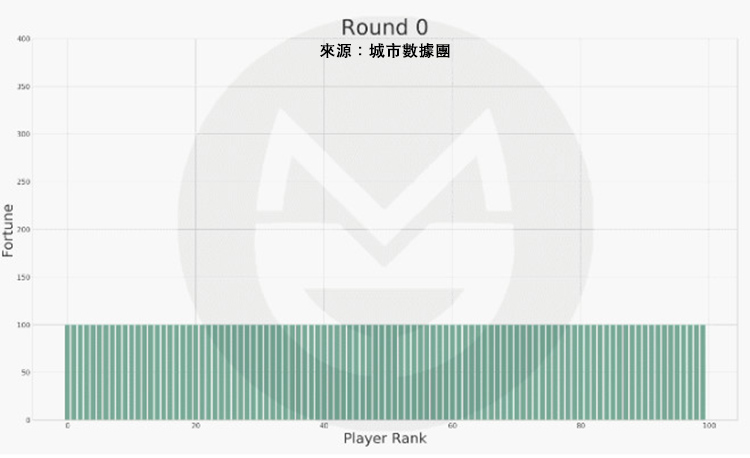
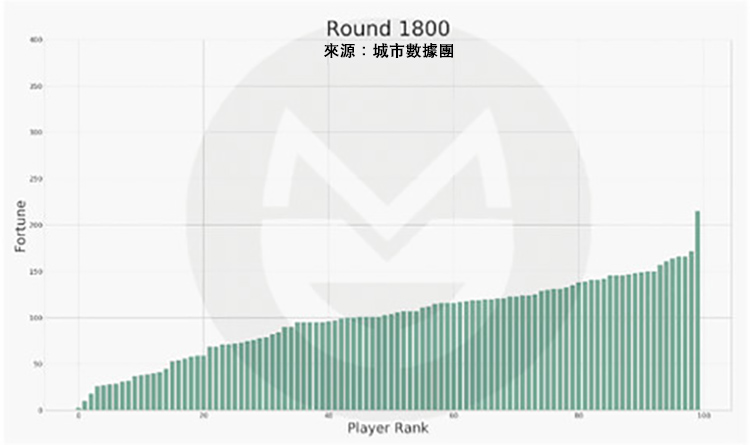
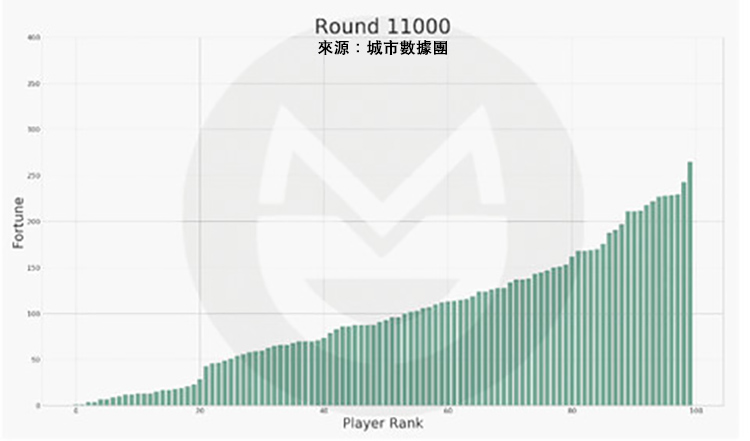
可以看到，每個玩家財富值的變動是極為劇烈的。為了方便描述整個社會財富的分配狀況，我們又按照財富值的排序做了一張圖，圖中橫軸標籤代表玩家排序（非編號），排序越高的財富越多。初始時所有人的財富值相等，隨著遊戲的進行，財富值差距越來越大。
第 0 次：
第 1,800 次：
第 11,000 次：
第 17,000 次：
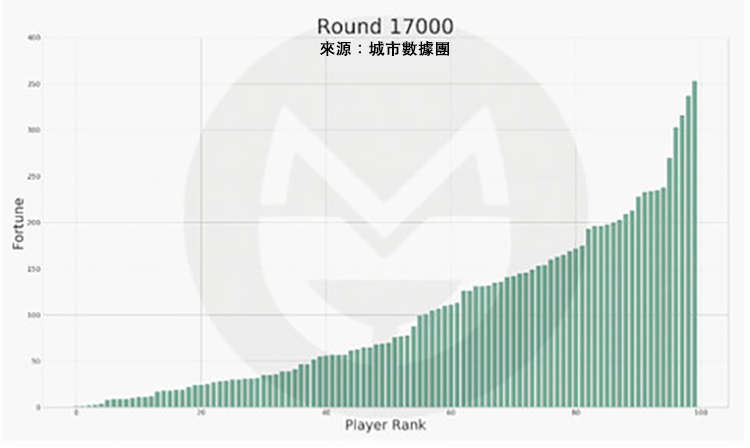
沒錯，財富的分配接近於冪律分佈（結論只是程序模擬，而非數學精確求解）。最後，社會將有很少的富人和很多的窮人：最富有的人的財富值約為初始財富的 3.5 倍；Top 10% 的富人掌握著大約 30% 的財富，Top 20% 的富人掌握著大約 50% 的財富；60% 的人的財富將縮水到 100 元以下。
就這樣，大部分人的錢跑進了少部分人的口袋裡。即使在最公平的規則下，世界依然展現出了殘酷的一面。
在此基礎上，我們又設計了更多的情景，同樣用程序進行了模擬。
允許借債會讓世界變得好一點嗎？
在現實社會中，情境會更複雜一些。比如說，當我們沒錢了，還可以找親友、找銀行、找投資人借債，說不定哪天就東山再起了呢？在允許借債的情況下，遊戲結果如下（排序後結果）：
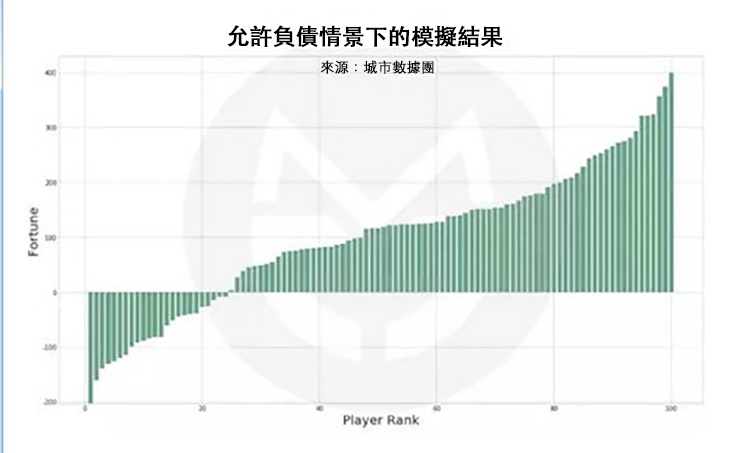
結果表明：遊戲結束時，最富有的人的財富值約為初始財富的 4 倍；Top 10% 的富人掌握著大約 33% 的財富，Top 20% 的富人掌握著大約 56% 的財富；大約 25% 的人背負著債務，最高負債約為 200 元。
沒錯，借債雖然能讓我們在走投無路時多一些周轉餘地，但最終會讓窮人變得更窮。
真能逆襲嗎？
我們以所有玩家財富值的標準差來衡量社會貧富分化程度，按時間序列做出圖來長這樣：
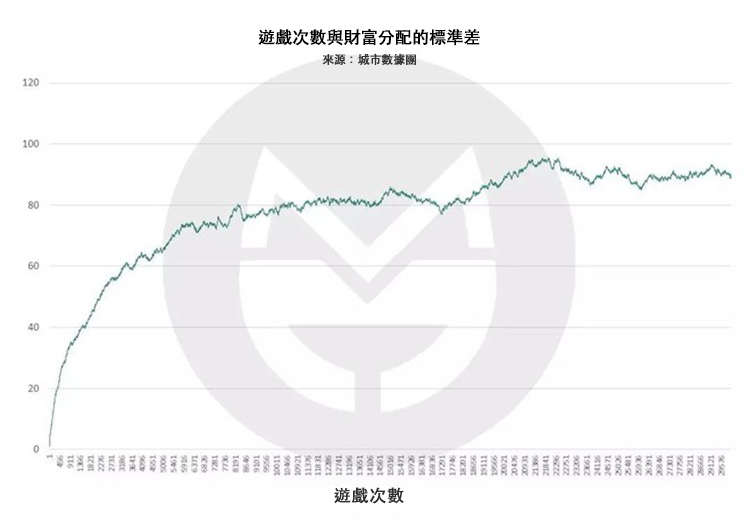（說明：橫軸表示遊戲輪數，縱軸表示社會財富的標準差）
可以看到，遊戲早期的標準差變動最為激烈，而在 6,000～6,500 輪遊戲後，標準差的變化趨於平緩，也就是社會財富分佈的總體形態趨於穩定了。按照我們設定的遊戲與人生的對應規則，這時玩家年齡為 35 歲。
這個結果告訴我們，35 歲之前，人與人之間的差距已經完全拉開了。
進一步看，如果一個人在 35 歲時破產，還有沒有可能逆襲呢？
本次模擬結果中，有 15 個人在 35 歲的最後一天時處於破產（負債）狀態，而他們在此後的財富值及排名如圖所示：
第 6,500 次：
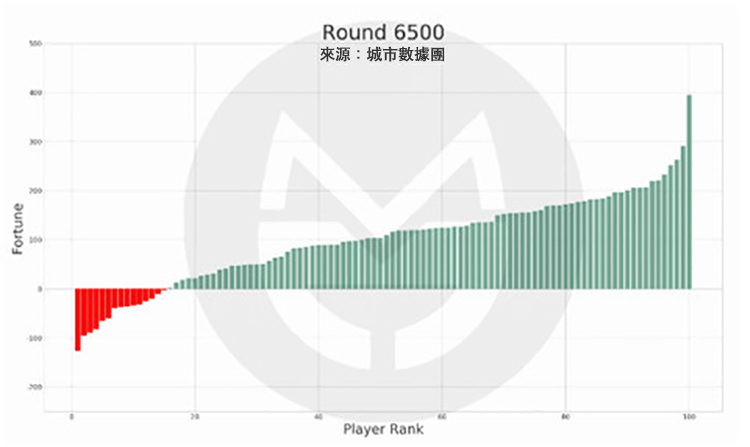
第 13,800 次：
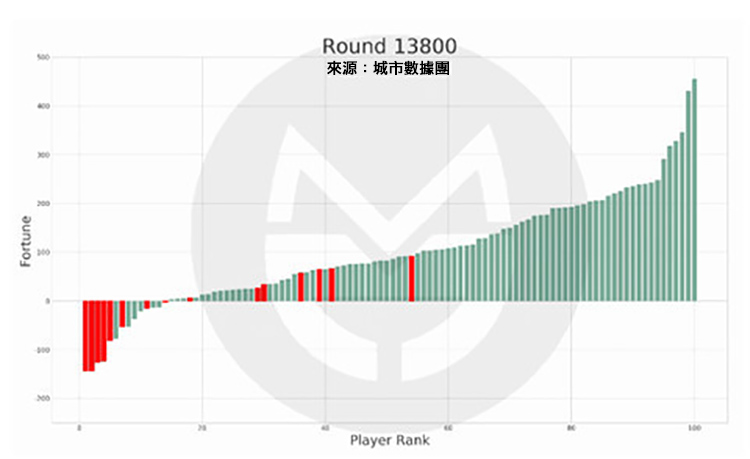
第 17,000 次：
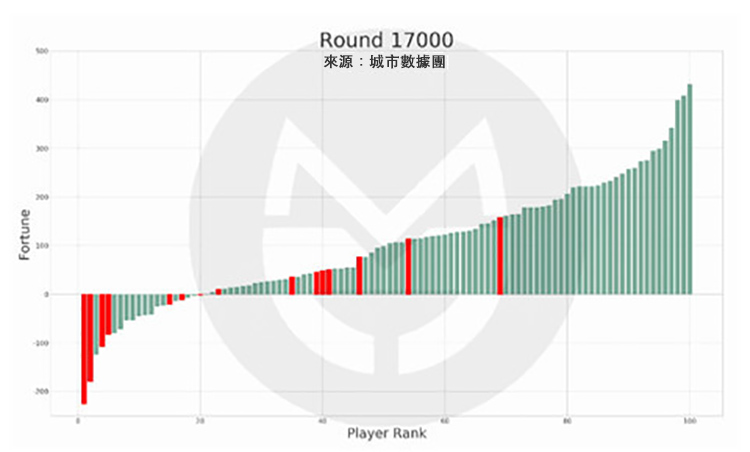
圖中的紅色柱子為在 35 歲時破產的玩家，綠色柱子為其他玩家；紅色柱子在縱軸上的高度變化表示其財富值變化，在橫軸上的位置變化表示其排名變化。
可以看到，當這 15 個人在 65 歲退休時，有 7 人仍然處於破產狀態，有 8 人還清債務並有了財富積累，但離富豪仍有相當差距。
看來，以 35 歲為界，雖然破產以後，仍有一半機率回覆到普通人的生活，但想要逆襲暴富，卻是相當困難的。所以，發財要趁早，大齡魯蛇逆襲更像是一個傳說。
富二代和普通人有什麼區別？
在真實社會中，每個人的起點其實並不相同，總有一些富二代、富三代，在財富遊戲的開始就占盡了便宜，這一點也應該被考慮到我們的模型中。
為了簡化計算，我們假設只有兩類玩家：90 個普通玩家（設定同上）＋10 個富二代玩家。富二代玩家的初始財富是 500 元，他們在每輪遊戲中需要拿出 2 倍的錢，同時獲得財富的機率也是普通人的 2 倍。遊戲結果如下圖（排序後結果）：
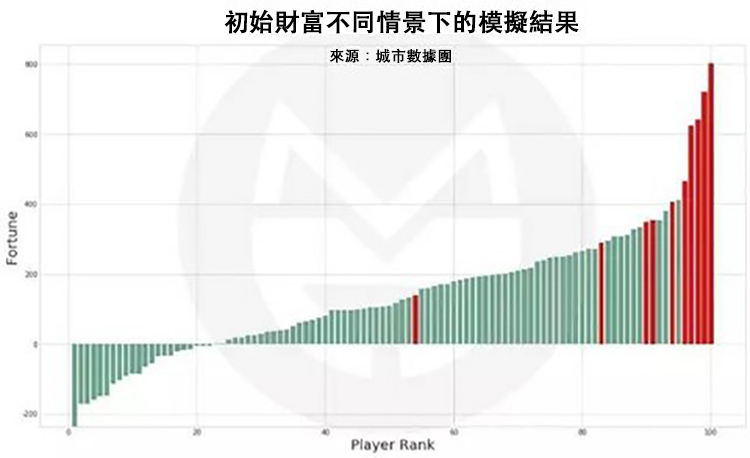（說明：上圖中的紅色柱子為富二代玩家，綠色柱子為普通玩家）
雖然這個分佈形態與全是普通玩家的結果基本一致：Top 10 和 Top 20 的富人掌握的社會財富比例和負債的人數比例都差不多，但是仔細來看，Top 5 富人中的全部，以及 Top 10 富人中的 7 位都是富二代玩家。
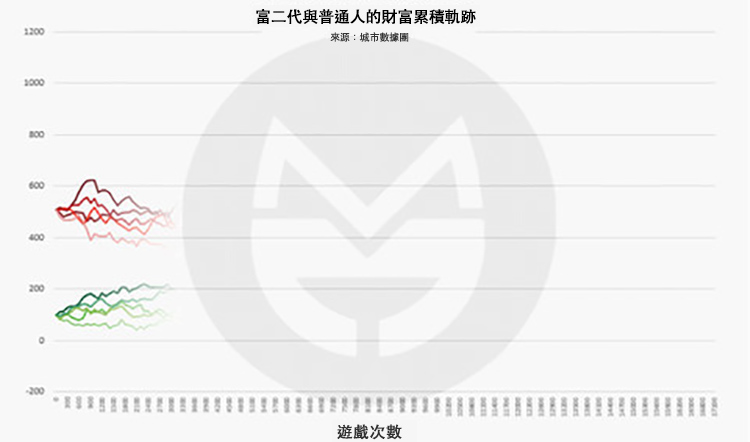
我們在富二代玩家（紅色線條）和普通玩家（綠色線條）中各選 5 位，繪製出他們的財富值變化圖：
第 0 次：
第 2,400 次：
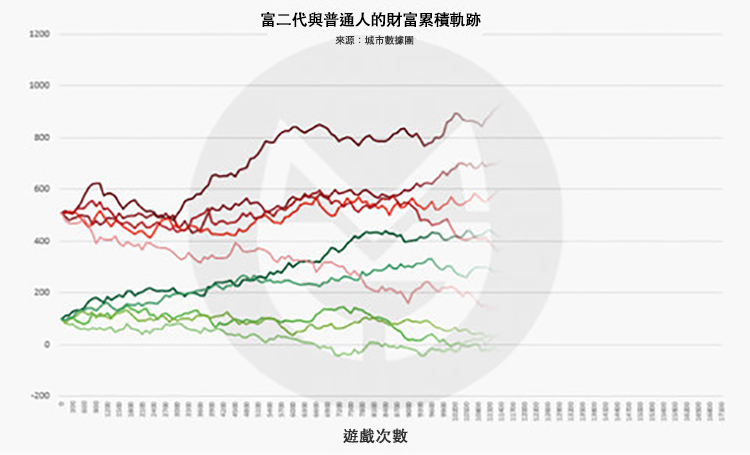
第 12,000 次：
第 17,000 次：
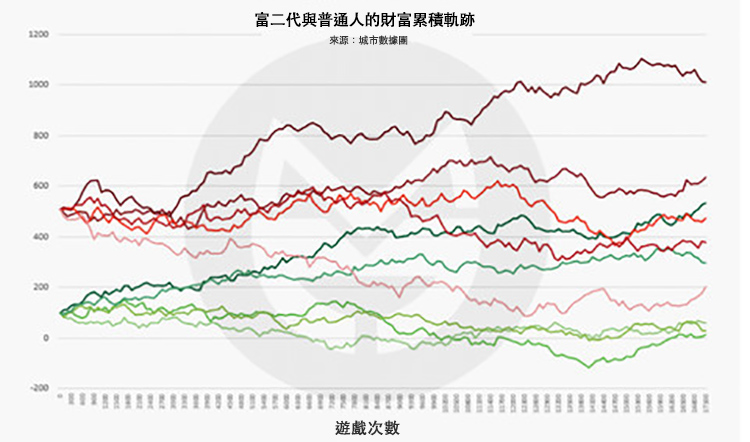
可以看到，富二代玩家中雖然也有 “敗家子”，但他們仍有很大機率將財富值維持在較高水平。富二代們和普通人生活在兩個世界中，偶有交集而已。
沒錯，普通人要有極好的運氣，才能到達與敗家富二代相同的高度。
對富人徵稅會改變財富分佈嗎？
為了緩和貧富分化帶來的諸多矛盾，在真實社會中有許多轉移支付的手段，稅收就是其中一種。
本輪遊戲中，玩家的初始財富同為 100 元，每輪遊戲中玩家獲得 1 元錢的機率相等，但若被選中的玩家在該輪遊戲時的財富值高於 200 元，則他只能獲得 60% 的收益；而另外 40% 的收益將平分給財富值低於 0 元的所有玩家（相當於破產者的最低收入保障）。模擬結果如下圖所示：
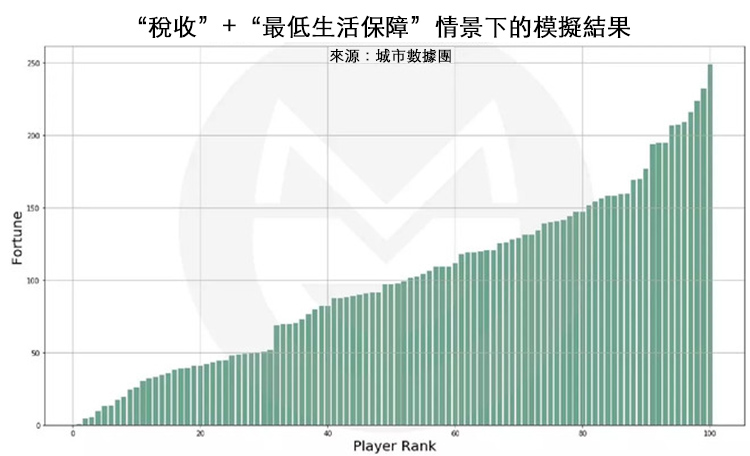
可以看到，在 “稅收＋最低收入保障” 的遊戲規則下，社會財富分佈仍然是高度極化的，區別只是基本消滅了破產者，同時富有的人沒那麼富了而已。
收稅可以平緩世界的分化，但是並不容易改變世界的殘酷本質（除非大大加強轉移支付的力度）。
努力的人生會更好嗎？
我們中的絶大多數人，沒有一飛衝天的發財運氣，也沒有腰纏萬貫的爹，更不甘於吃最低收入保障。想要改變命運，我們只能選擇自己更努力，去爭取更好的生活。
我們假設每個玩家的初始財富仍然為 100 元，但有 10 人比別人加倍努力，從而獲得了 1% 的競爭優勢，即贏得收益的機率比別人高出 1%，模擬結果如何呢？
第 0 次：
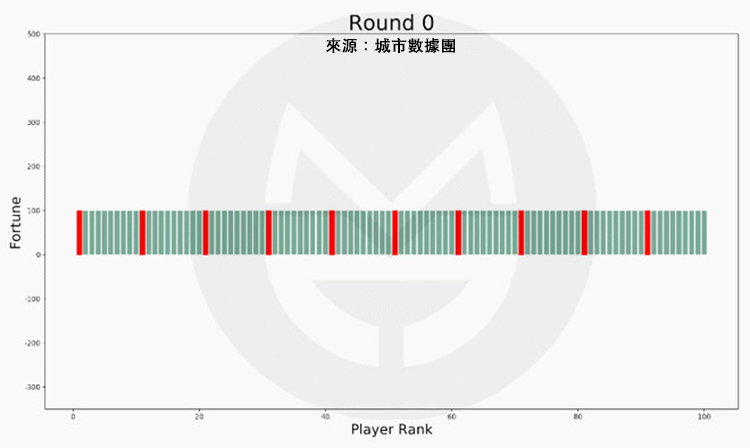
第 9,200 次：
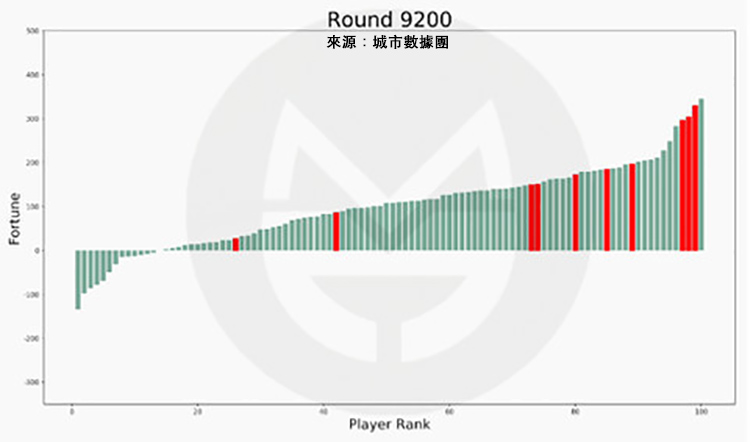
第 16,100 次：
（說明：上圖中的紅色柱子為更努力的玩家，綠色柱子為普通玩家）
可以看到，社會財富的總體分佈形態沒有什麼變化。但是，10 位努力玩家中的 9 位都進入了富人 Top 20！
是的，儘管最成功的玩家不一定是最努力的那個，但是努力的人大都混的還不錯。感謝這個殘酷世界還給我們留下一條生路。
看到這裡，相信各位讀者已經對這個問題有了自己的答案：該如何面對這個殘酷的世界？那就是努力並堅持下去。
《雪球》授權轉載
【延伸閱讀】
55539
