收益法是將未來金額(現金流量或股利)予以折現,取得目前之現值的一種評價方法,是投資學的 ABC、專業投資圈的必備,但需預測未來、參數假設多、運算繁複,且未理會市場情緒,普羅投資圈多半不能(要取得未上市公司之財務及相關資訊進行預測是有難度的)、不愛也不信。
實務上,收益法因主觀假設多、評價結果紛歧、討論空間大,非必要能免就免,所以多用於涉及控制力或影響力的併購交易。
FVM 教材對收益法之指引,以「現金流量折現法(Discounted Cash Flow method, DCF)」為核心,兼及「股利折現模式(Dividend Discount Model, DDM)」,與兩個對應的簡化模式:固定成長 DCF―資本化模式(Capitalization model)、固定成長 DDM(Constant-growth DDM)。
其中,最難的是 DCF 模式,得先預測各期的「自由現金流量(Free Cash Flow, FCF)」;最簡單的是固定成長 DDM 模式――穩定發放股利是大部分經營者願意的,且現金股利也較容易預測。
現金流量折現法
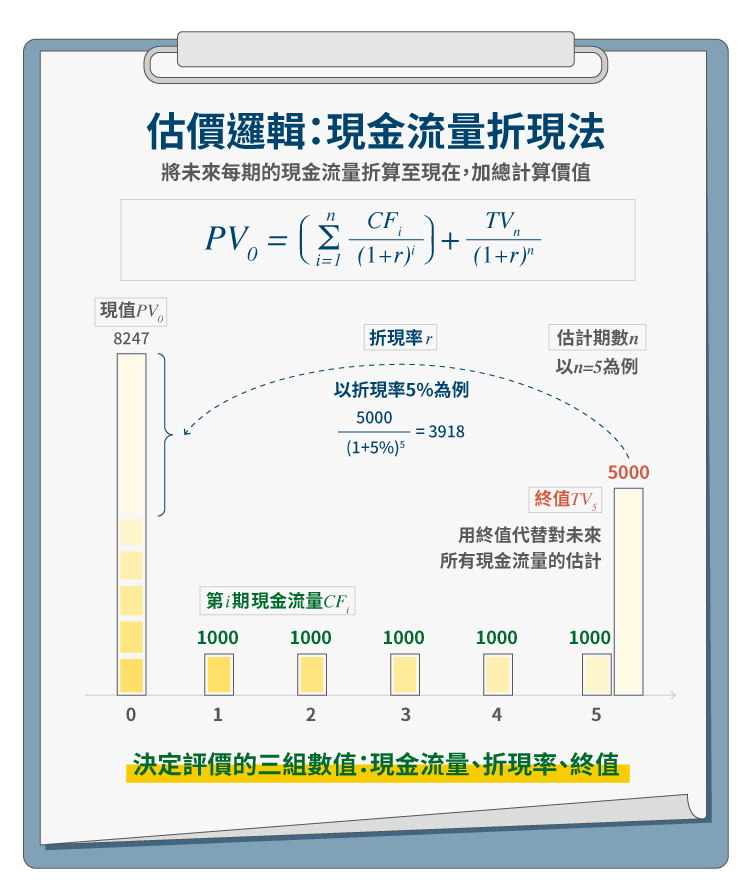
DCF 模式的基本技術,就是折現:現值公式為 \(PV_0=(\sum\limits_{i=1}^n\frac{CF_i}{(1+r)^i})+\frac{TV_n}{(1+r)^n}\)。只要決定三組數值,就能完成評價:現金流量(Cash Flow, CF)、折現率(r)、終值(Terminal Value, TV)。其中因為我們不可能預期公司每年的現金流量,但公司又是假設永續經營存在,在此前提下,理論上應該對永續的現金流量做折現。
然而實務上光估計 2、3 年的 CF 就涉及許多假設及判斷,何況超過 5、6 年。為了解決前述困擾,我們多採兩階段 DCF 模型,第一階段為較嚴謹的估計 CF;第二階段用終值代替對未來所有現金流量的估計。
此處所使用的 CF 較特別,不是直接取用現金流量表上的「營運活動之現金流量(Operating Cash Flow, OCF)」,而是 OCF 扣除維持成長必要的資本支出(Reinvestment Requirements, RR)與搭配投入的淨營運資金增額,即「自由現金流量(Free Cash Flow, FCF)」(實務上 FCF 並不是 IFRS 規範項目,計算公式因人而異有許多版本)。
此外,與市場法一樣,運用 DCF 模式也得先搞清楚要用何種評價基礎:股權價值(直接)或企業價值 EV(間接)?各有各的配套變數,不能混搭。若直接評價股權,則所需的 FCF 須扣除借款成本(FCF to Equity, FCFE),而所用的折現率是考慮股東的權益資金成本(Cost of Equity, \(k_e\))。
反之,就要使用企業整體營運所創造的 FCF(FCF to Firm, FCFF),並搭配股東及債權人的資金成本,即為加權平均資金成本(Weighted Average Cost of Capital, WACC)。DCF 在不同評價基礎下的變數比較,如下表所列。

各變數之公式如下:
\(FCFF=EBIT\cdot (1-t)+\) 折舊及攤銷 \(-(RR+\) 淨營運資金增額 \()\)
\(FCFE=FCFF-\) 利息費用 \(\cdot (1-t)-\) 本金償還 \(+\) 新增融資款
\(WACC=\frac{D}{D+E}\cdot (1-t)\cdot k_d+\frac{D}{D+E}\cdot k_e\)
\(D\):債務之公允價值
\(E\):股東權益之公允價值
\(k_d\):債務資金成本
\(k_e\):權益資金成本
\(t\):企業所得稅稅率
至於終值(TV),則有兩種估計方法。採用簡化的固定成長 DCF 模式或找一個「退出乘數(exit multiple)」評估當時價值。前者仍循收益法,後者則改依市場法:找可類比公司、訂乘數。很顯然,後者混用評價技術,內部邏輯不太一貫,前者為佳。所以終值暫以資本化模式計算,列式如下:
採 EV 評價基礎之終值:\(TV_{ev}=\frac{FCFF_{n+1}}{WACC-g}\)
採股權評價基礎之終值:\(TV_v=\frac{FCFE_{n+1}}{k_e-g}\)
其中:\(g\) 為終值之永久性成長率
將前述變數帶入折現通式時,在採 EV 評價基礎作法下,DCF 模式就成了如下公式:
\(EV_{op}=\sum\limits_{i=1}^n \frac{FCFF_i}{(1+WACC)^i}+\frac{1}{(1+WACC)^n}\cdot \frac{FCFF_{n+1}}{WACC-g}\) ⋯(1)
但需注意,由於 FCFF 是未來營運現金流量之預估,自然不包含非營運資產負債之營運績效,因此,需再加上非營運之資產與負債,才能得到完整的企業價值(或是股權價值)。
\(EV=EV_{op}+\) 非營運資產公允價值 − 非營運負債公允價值 ⋯(2)
\(E=EV-D\) ⋯(3)
若採權益價值基礎則更簡單,只須將(1)式中的 WACC 換成 \(k_e\)、FCFF 換成 FCFE 即可,最後也不需扣除負債。
整個模式,最難的就是資金成本,此為 FVM 教材最占篇幅之議題。由於間接法的 EV 基礎考量較廣,故以下就直接以間接法說明。
參數 1、債務比重
由於評價是公司的長期價值,因此 WACC 所用的權重(債務比率)並非現時的狀況,而是公司理想的長期最適財務結構。通常,可採用產業平均的財務結構。但若該被投資公司之融資能力、信用狀況與產業差異甚大時,就得另行調整。不論如何,產業平均是一個必須使用的參考依據。
參數 2、權益之資金成本
在針對現金流量折現時,挑選適當的折現率極為重要,一般而言,多數人選擇使用標準的資本資產訂價模式(Capital Assets Pricing Model, CAPM)1或其簡單的變異。此時面臨的問題至少有三:要估計市場風險貼水、要選擇適當的無風險利率、要決定 beta(以下簡稱 \(\beta\))。
註:1其他計算權益資金成本的方法如套利定價理論(Arbitrage Pricing Theory)及三因子定價模型(Three Factor Model)。
很糟糕的是,財務學家發現這三項數字都是會隨時間變動的。顯然,一般作法的假設(市場風險貼水、無風險利率及 \(\beta\) 都不會隨時間改變),並不符合實際狀況。此時,必須考慮 Time-Varying Expected Returns 下的作法。這種方法相當複雜,暫時略過。
FVM 教材,對於權益資金成本(\(k_e\))的估計,僅介紹最傳統、最簡單的 CAPM。依 CAPM,權益的資金成本如下:
\(k_e=r_f+(r_m-r_f)\cdot\beta\) ⋯(4)
\(r_f\):無風險利率(risk-free rate),對無風險資產期望的報酬率
\(r_m\):投資人要求的市場報酬率(required market rate of return),對一個充分風險分散之投資組合之預期報酬率
\(r_m-r_f\):投資人要求的風險貼水(required equity premium)
\(\beta\):單一資產的系統風險係數
雖然是傳統的投資學理論,但 FVM 教材,仍提到不少細節,值得參考。以下分述。
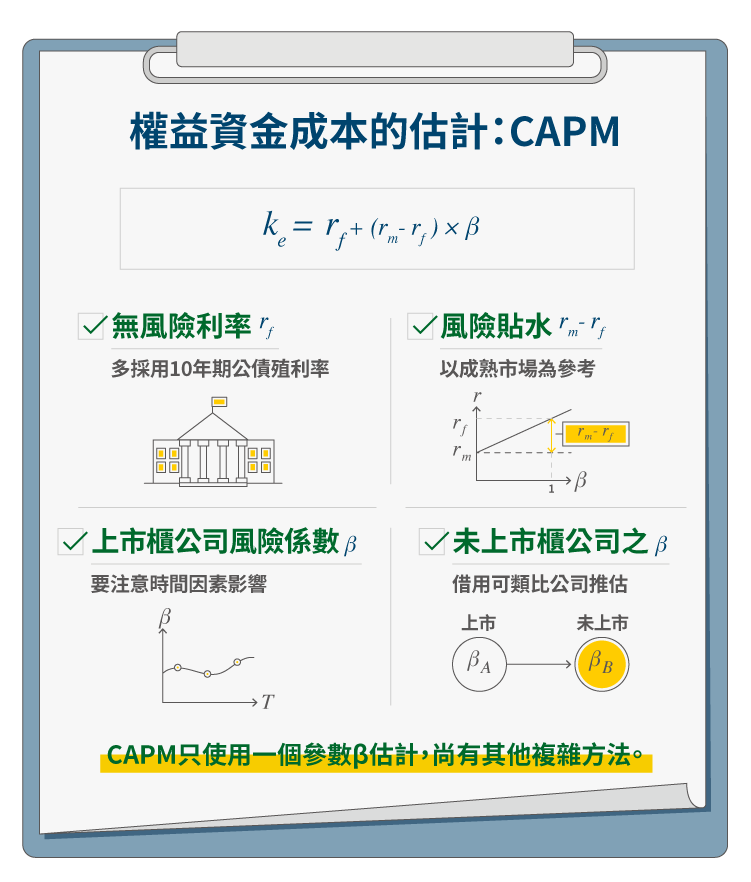
- (2-1)無風險利率:\(r_f\)
通常,無風險利率來自公債;需注意,所採用的公債幣別、期間與所持有之股票是否有錯配狀況――幣別不同、存續期間差異過大。
實務上,在進行股票評價時,針對無風險利率,國外多採用 10 年期或 20 年期的公債殖利率,因股票產生的現金流量的存續期間長。在我國多採用台灣政府 10 年期公債殖利率,主因 10 年期公債的交易非常活絡,數字具有代表性,故以 10 年作為一折衷的期間(也有學者建議應該用長期(如 20 年)的平均 10 年期公債殖利率當作無風險利率)。
另外,也有不少人以定存利率當作無風險利率,但這在評估股票價值時,較不適宜當成 CAPM 的無風險利率,主因為定存的期限通常較短,且反應資金供需較不靈敏、不即時。
- (2-2)上市櫃公司風險係數:\(\beta\)
\(\beta\) 應為前瞻性(forward-looking estimate),而非歷史 \(\beta\)。常見以歷史 \(\beta\) 作為替代,所隱含的假設是:未來的波動與過去類似;換言之,若此假設不成立,就該進行前瞻性 \(\beta\) 之估計。至於前瞻性 \(\beta\) 如何估計,FVM 教材僅以選擇權市場帶過,實則極為複雜。
須注意的是,由於許多學者發現 \(\beta\) 有隨時間改變(time-varying)的現象,因此就算是使用歷史 \(\beta\),也需要經過調整方可使用。另外,運用迴歸分析推估歷史 \(\beta\) 時,期間長短決定於所搭配的資料頻率與資料品質:
―若年度夠長,採月資料、週資料頻率即可(原則上,日資料雜訊過多)。一般來說,會採用過去 2~5 年的歷史資料推估 \(\beta\);若僅用 2 年資料,多採週報酬;若估計期長達 5 年,就可能採月報酬。
―若市場波動過大,就會拉長期間,以免受短期波動之扭曲。
- (2-3)未上市櫃公司之 \(\beta\)
既已推估出上市櫃公司之 \(\beta\),接著就可利用可類比公司之概念,進一步推估未上市櫃公司的 \(\beta\)。由於 \(\beta\) 代表的風險有兩類:營運風險與財務風險。可類比公司僅是營運風險類似(有相似之風險、成長及現金流量特性),財務風險則未必。
因此,在借用可類比公司之 \(\beta\) 時,若長期資本結構(財務風險之主要指標)差異太大時,就該用 Hamada 公式來調整差異,詳細步驟在此略過。另外,FVM 教材要求 \(\beta\) 要自行估算,若要引用外部資料,應引用同一來源。
- (2-4)風險貼水:\((r_m-r_f)\)
市場期望的風險貼水,也是前瞻性,理應由歷史資料作為推估起點。但 FVM 教材對新興市場的推估說明,較新鮮――以成熟市場作推估。不過,依我們的看法,台灣市場發展應算成熟,實務上不需調整。
根據研究,新興市場可能缺乏足夠資料或波動過大,不宜直接採用其歷史的風險貼水來推估期望的市場貼水。研究建議以成熟市場之風險貼水,推估新興市場,詳細方法在此省略。
- (2-5)CAPM 之限制
CAPM 的基本假設是,個別股票風險及預期報酬與系統風險(systematic risk)呈線性相關。因其假設過簡,常受批評。其中的批評之一就是只有一個 \(\beta\),風險涵蓋面太小,未納入其他重大風險考量,如規模大小、現金流量波動、流動性等。議題甚多,待有機會再行介紹。
參數 3、債務資金成本
相對於權益資金成本,債務資金成本就簡單得多。如果目前的財務結構接近長期最適的財務結構,則可以近期舉債成本(recent borrowing)作推估,作為推估起點。原則上,要加上增額借款、再融資之考量,當然,也可參考可類比公司之資料。
另外也可採信用價差作長期推估,信評越差的公司舉債利率與無風險利率的差距就越大,實務上還需考量不同國家與通膨等問題。不管採取何種方式,總要符合市場參與者的長期最適之預期。
固定成長 DCF―資本化模型
面對這複雜的 DCF 模式,實務自然發展出一個簡化模式:資本化模型。假設 FCFF 會以一個固定比率永續成長,資金成本也是一個常數,則其評價就可簡化成:
\(PV=\frac{FCFF}{WACC-g}=\frac{FCFF}{c}\)
此式延續 DCF 之處理,且成長率必定不超過資金成本。此模式雖易用,假設卻不實際,故多半用來與其他評價技術做交叉比對之用。
股利折現模式

比起 DCF 模式,股利折現模式(DDM)更常用,因其較直覺,且股利較易預估。基本觀點是:今天的股價就是未來現金股利之折現總和,其估算如下:
\(P_0=\sum\limits_{i=1}^\infty \frac{D_i}{(1+k_e)^i}\)
\(P_0\):評價日之評價結果
\(D_i\):預期第 i 期發放之現金股利
要適用此模型,顯然有個假設:公司一定會發放股利,否則一家從不發放股利的公司其公允價值會誤為 0。
另外,假設股利的發放型態是固定成長(包含零成長),則評價模式可以再簡化為固定成長 DDM,即為高登成長模型(Gordon growth model):
\(D_i=D_{i-1}\cdot (1+g)=D_0\cdot (1+g)^i\)
\(P_0=\sum\limits_{i=1}^\infty \frac{D_0\cdot (1+g)^i}{(1+k_e)^i}=\frac{D_0\cdot (1+g)}{k_e-g}=\frac{D_1}{k_e-g}\)
同樣地,此推導式要能收斂的前提還是,股利成長率不能超過資金成本。
結語
收益法的基本概念雖然簡單,但實際計算時會遇到大量需要評估的參數,每個參數又有各自所需的調整方法,要注意的細節很多,對於一般投資人來說不是那麼平易近人。此文僅就大方向的邏輯概念力求清楚介紹,有興趣的讀者可對於文中各種議題繼續深入研究,相信對於估值的功力會有所增進。
【延伸閱讀】

















