銀行體系的運作與貨幣創造 

剛上大學時申請就學貸款；Iphone 出了最新款，跟銀行申請一筆信貸補足不夠的金額；或是出社會幾年後想要買房子而跟銀行借了房貸。在我們的社會運行中， 人的一生會有很多跟銀行接觸的機會，跟銀行有金錢借貸往來也是許多人都有過 的經驗，但你知道嗎?在我們的經濟運行中，社會上的錢會「愈借愈多」哦! 

想像今天 Selina 在 A 銀行存了 1,000 元，A 銀行將 1,000 元全部借給 Hebe， Hebe 把借來的 1,000 元全部存進 B 銀行，B 銀行再將 1,000 元借給 Ella，Ella 又將 1,000 元全數存進 C 銀行，以此類推……。原本只有 Selina 的 1,000 元， 透過銀行的借貸效果後，變成 Selina 在 A 銀行存有 1,000 元，Hebe 在 B 銀行 存有 1,000 元，Ella 在 C 銀行存有 1,000 元，光是 SHE 在社會上就有了 3,000 元的存款。 

當然，社會上的錢不可能這樣的無限增加，萬一 SHE 同時都要提領自己的 1,000 元，銀行是無法支付的。所以央行為了金融體系能正常運作，規範每間銀行在收 受的存款中，不能全數貸放出去，必須保留部分金額，當其他存款戶需要提領時， 

銀行能夠正常返還存款。銀行收受存款而必須保留的部分金額，就是銀行準備金的概念，央行規定銀行存款必須保留多少準備金的比例，稱作法定準備金比例。 

你的貨幣是什麼貨幣? 

為什麼一開始 Selina 擁有的 1,000 元，在透過銀行的存貸後能夠變成 SHE 的 3,000 元?其中關鍵在於貨幣的定義。 

一般我們直接持有並流通的現金，經濟學中有個比較複雜的名字，叫做通貨淨額， 又稱 M₀。

但手中拿的是錢，存在銀行的也是錢，你知道你的錢是什麼錢嗎?。如果 M₀ 加上銀行活期存款，這是 M₁ 的定義。 

M₀ = 通貨淨額 

M₁ = M₀+銀行活期存款 

央行雖然一開始只發行了固定數額的鈔票(M₀)，但透過銀行的借貸活動進行，整體社會的銀行存款(M₁)增加，錢也就「愈借愈多」了。 

錢能增加到什麼地步? 我們與貨幣的距離是? 

現在我們知道銀行必須保存部分準備金，避免存款戶無法提領現金的風險，也知道透過銀行借貸行為，能夠使社會中的 M1 貨幣增加。然而因為央行對銀行準備金有其限制，使得 M1 貨幣雖能隨借貸增加，但仍有上限。 

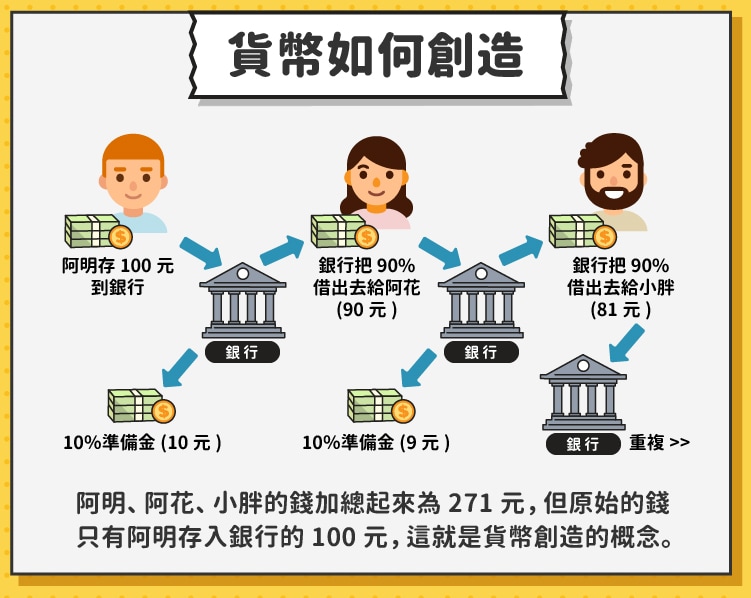
現在我們假設法定準備金比例為 10%，且銀行會將剩餘的存款全數貸出，而獲得貸款的民眾會再將全數金額存進另一銀行。 

一開始 A 銀行有存款 100 元，提存 10 元的準備金，將 90 元全數貸出；B 銀行獲得 90 元存款，提存 9 元的準備金，貸出 81 元；C 銀行獲得 81 元存款，提存 8.1 元的準備金，貸出 72.9 元 …，以此類推我們可以獲得如以下的表格。 

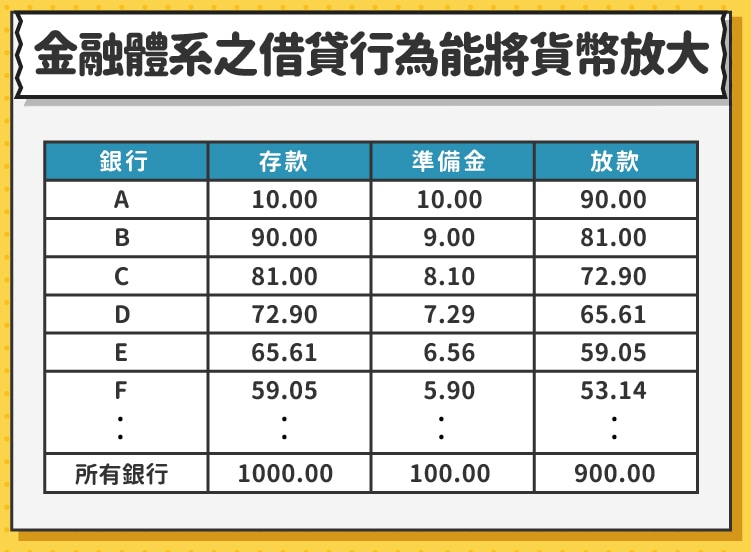
一開始 A 銀行的存款 100 元，透過銀行間持續存款、貸款的效果，最後社會上的總存款增加為 1,000 元。不知道你有沒有發現，存款貨幣增加了 10 倍，剛好是法定準備金比例 10% 的倒數，然而這個關係可不是巧合喔! 

簡單運用高中數學等比級數的概念，我們可以得到總存款 = 100+90+81+…= 100/(1-90%) = 100/10% = 1,000 

在經濟學中我們定義: 

貨幣基數（MB） = 通貨淨額（M_0） + 準備金（R） 

貨幣數量（M）與貨幣基數（MB）的關係為 M = m × MB 

m 為貨幣乘數，也就是貨幣基數理論上能夠創造出貨幣數量的最大倍數，而貨幣乘數正好就是法定準備金比例的倒數，如上例的貨幣乘數就是 1/10%=10 倍。也就是說，一開始擁有 100 元的貨幣基數，在法定準備金比例為 10% 的情況下，最多能夠創造出 10 倍的貨幣數量。然而在現實生活中，銀行基於流動性管理的考量，會保有超額準備，並不會將法定準備金以外的存款全數貸出；而一般大眾因為日常花費的需要，也不會將全數的現金都存於銀行之中。實際上貨幣因借貸效果增加的倍數會小於貨幣乘數，貨幣乘數是貨幣創造的上限。而法定準備金比率也成為央行用來控制市場資金鬆緊的工具之一。當央行調降該比例，代表銀行能貸放出更多的資金，能增加市場資金的餘裕；反之，當央行調升比例時，意味著有較多的資金需提存於銀行之中，市場上的資金供給則變得較 為緊縮。下次當你到銀行借錢時，不妨問問銀行的法定準備金比例是多少，而你也有可能是讓貨幣「變多」的推手之一喔。 

【延伸閱讀】

• 不穩固的銀行體系：為什麼世界上大部分的銀行都面臨崩潰
• 掌握美國經濟的 Fed 成立原由是銀行體系的崩潰 ?